Effective altruists should be less concerned with downside risk measures than personal investors.
Provided you can become comfortable with volatility, effective altruist portfolios should be at least 100% stocks, and theoretically as high as 300% although the options for achieving this theoretical level of leverage appear limited. Small cap value stocks can be relied on to offer slightly more expected return than the broader market, and as such are appropriate for an effective altruism portfolio. In the past they have substantially outperformed, but whether this anomaly will continue isn't known. International diversification is a good thing, but far from essential for an effective altruism portfolio.
Because of the environment we are now in, which is likely to persist, stock returns are expected to be substantially lower than they have been in the past. Expected future stock returns involve considerable unavoidable uncertainty and much risk. Even over a 50 year period, there is a distinct possibility of obtaining a negative real return.
Personal investing is very different from effective altruism investing due to its greater downside risk aversion. Most of the recommendation made here are inapplicable to personal investing.
Effective altruists that earn to give put a lot of time into earning their money. It is therefore reasonable to spend a few thousands hours learning how to invest that money well. If you received all the money you planned to donate up front, then over a lifetime, the payback from investing well might be to increase your impact 3-fold or more. (See asset allocation article for the justification of this figure.) Granted receiving all the money you plan to donate up front is unrealistic, but still the benefits from investing well can be substantial.
Throughout this document I deal in real, that is, inflation-adjusted, terms. I also incorporate dividends into all returns. Reported returns are usually given in nominal, that is inflation unadjusted, terms, and reported stock index values normally exclude dividends.
For a variable return sequence it is important to understand the difference between the arithmetic and geometric mean. The geometric mean is widely quoted. For lognormally distributed returns, which is approximately true of the stock market, the geometric mean reflects the median outcome. Effective altruists, seeking to maximize the good they do, are however less interested in the median outcome, and more interested in the larger arithmetic mean outcome. This is a key difference between effective altruist investing and retirement investing. In retirement investing you are seeking to maximize, say, the 5th percentile worst outcome. Or if you are sophisticated, a weighted sum of the different percentile outcomes, but in any case heavily weighted towards the worst cases. In effective altruism investing the weight you place on the worst case outcomes is less.
Financial theory suggests that by treating your effective altruism tagged funds and your personal funds as one big bucket, and not two separate buckets, you will be better able to optimize. Financial practice suggests that it is hard enough to optimize the two separately, that you will never be able to optimize the two together. A possible compromise might be to optimize the two separately, but then look for complementarities in the results. A simple example: Your personal portfolio might be 60/40 stocks/bonds, and your equally sized effective altruism portfolio might be 100% stocks. It is then reasonable to hold a single 80/20 portfolio rather than have two separate accounts. The danger of doing this however is it is too easy to lose sight of which are the effective altruism tagged funds.
The higher the systematic volatility, the higher the expected return. Systematic volatility refers to volatility that can not be diversified away. There are no expected rewards for diversifiable volatility. Holding a single stock instead of the broad market is an example of diversifiable volatility. It is important to remember though that expected returns are just that. They may never be realized. It often isn't enough to simply wait a sufficiently long time. For a retirement investor volatility is the enemy. For the effective altruist seeking to maximize expected good, volatility can be their friend, since it brings with it increased expected returns. That is, whereas the retirement investor is reasonably risk averse, the effective altruist is less sensitive to risk.
For effective altruism causes, early money is often more valuable than late money. So, does it make sense to take out a personal loan for effective altruism causes? The answer is nearly always, no. There are two reasons. First careers, and future income are by no means guaranteed. This is true both because of the risk of ill-health and unfortunate circumstances, and because of technological change. Second, without assets to secure a loan, the interest rate charged will be very high, wiping out the benefits.
Asset allocation is the distrbution of a portfolio between different asset classes. As explained in Effective Altruism Investing Strategies: Asset Allocation in theory effective altruist portfolios should be heavily leveraged, comprising perhaps 300% stocks and -200% cash. There are many problems associated with this:
There are no expected rewards from holding diversifiable risk, so you should diversify. Although the benefits of diversification are less for an effective altruism portfolio than a retirement portfolio. The minimum number of stocks needed for a diversified portfolio is probably around 50. Realistically, this can most readily be done by holding mutual funds, not by purchasing individual stocks.
98% of all New York Stock Exchange trading is performed by institutional investors. So you can bet that the counterparty to any trade you place is an institutional investor. They have been in the game far longer than you, know how assets are priced better than you, are able to hire the smartest brains in the industry, and are able to respond to market imperfections in milliseconds, having far bigger and faster computers than you do. Your only chance of winning is by not playing the game. To buy and hold rather than actively trade.
History shows it is not possible to pick ahead of time mutual funds that will outperform their benchmarks after expenses. Some mutual funds do show slight out-performance before expenses, but they more than compensate for this after expenses. Index funds attempt to replicate the benchmark at as low an expense as possible, and as such are highly recommended.
Exchange traded mutual funds, or ETFs, are bought and sold by retail investors at a price set by the market throughout the day, while traditional mutual funds have a fixed price that is set once per day. The difference between ETFs and traditional funds is largely irrelevant to the effective altruist.
The small cap value segment is slightly more volatile than the broad market. As a result we would expect it to have slightly higher expected returns. It turns out it had much higher returns over the period 1927-2016. And, importantly, also over the period 1995-2016, after the small cap value effect was widely publicized by Fama and French. The much higher returns after the effect was widely publicized could just be a statistical fluke, but beta, the slightly higher expected returns on account of higher systematic volatility is something that can be reliably expected going forward. Thus small cap value seems highly suitable to effective altruism portfolios. The downside is market tracking error. There will be years when the broad market is up, but small cap value is down significantly.
In recent years there has been an explosion of additional factors, besides size (publicized: 1981, 1992) and value (1983, 1992), such as momentum (1997), profitability (2006, 2013), quality, investment, and low volatility. Unfortunately many of these factors lack strong theoretical underpinning for why they exist, and equally important, too short a time exists after they have been widely publicized to know if they will continue. Nonetheless, they warrant monitoring to see how they perform over the next few decades.
Stocks are positively correlated with economic expectations, while some effective altruism causes are inversely correlated with the economy. Global poverty, for example, is inversely correlated with the global economy. This means that when there is a recession, and there is greater need, the resources available in effective altruism portfolios will be at their lowest. More important than correlation though is covariance. Because stocks represent a contingent claim on economic output after labor and bond holders have been paid, stocks are far more volatile than economic expectations. When the stock market dropped 57% over 2007-2009, expected living standards of the poor in Africa and Asia were not cut in half. In any case, the issue is not whether the resources are sufficient to match the cause, but donating to do the most expected good. The impact of a donation to combat global poverty of a particular size is likely to be only slightly greater during a recession, while the expected gains from taking on risk in a portfolio are substantial. Therefore even for causes that are inversely correlated with the economy, a 100% stocks portfolio makes sense.
It is desirable to invest internationally for the diversification benefits it brings. However, having a fully diversified global portfolio shouldn't be seen as some sort of holy grail, that must be obtained. This is especially true for an effective altruist who is less concerned about managing risk, and more concerned about doing the greatest good. International equity investments are often available hedged or unhedged against foreign currency fluctuations. While hedging might make sense for a retirement portfolio, it makes little difference to an effective altruist.
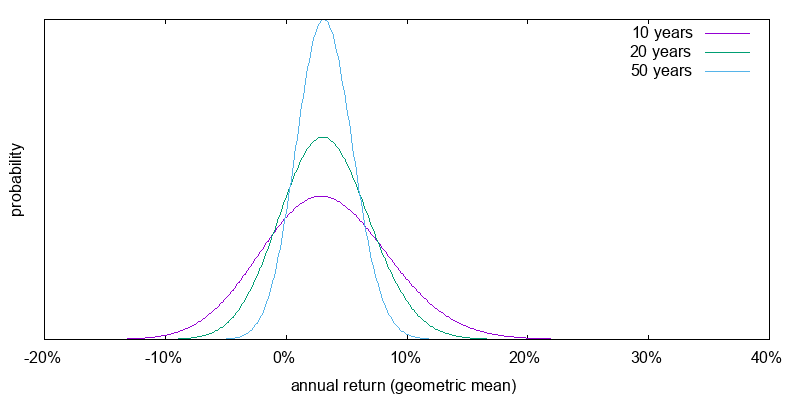
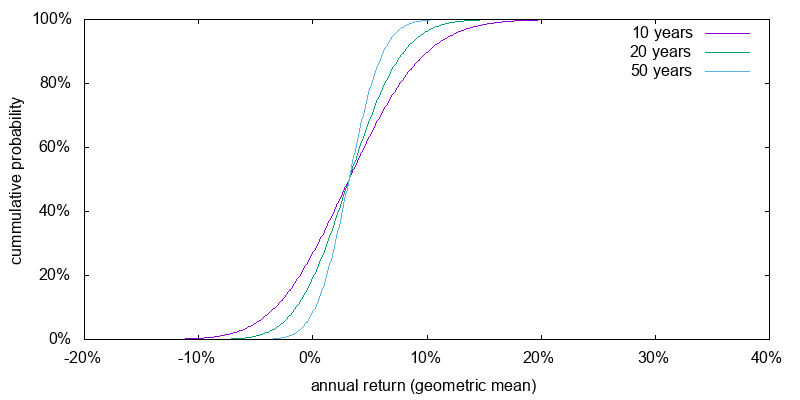
In finance volatility is usual a synonym for standard deviation. The volatility of stocks is large. From 1900-2000 the volatility of a weighted World stock market was 17.0%, and the U.S. stock market was even more volatile. We only have around 100 years of reasonably accurate stock market data. This means that, even if the financial processes generating the stock market returns are unchanged, the uncertainty in our estimate of the mean return, the standard error, is huge. For independent identically distributed returns the standard deviation of the sample mean is inversely proportional to the number of samples. Thus, based on 101 years of data, the standard error is 1.7%. We can be 95% confident that the true population mean return lies within two standard deviations, or plus or minus 3.4%. This inaccuracy, a 6.8% range for the mean return, is very unsettling, but it is something we have to live with.
Ignoring heavy tails, financial returns are approximately lognormal. This means the median value is equal to the geometric mean. The geometric mean is calculated from the arithmetic mean R, and standard deviation σ:
I construct reasonable return estimates going forward for stocks, small cap value, and a 60/40 portfolio of stocks/bonds. The U.S. was one of the lucky countries in the previous century. There is no reason to believe this will continue in the present century. So it is important to factor in the World experience when making market predictions. According to Dimson, Marsh, and Staunton, a weighted developed world index for 1900-2000 returned 7.2% annual arithmetic mean and 17.0% annual volatility. During this period they report the risk free rate on short-term U.S. Treasury notes was 0.9%. In March 2017, we are in a very different interest rate environment, and one that appears likely to partially persist for the foreseeable future. The risk free rate is 0.56% nominal and the 2017Q1 Survey of Professional Forecasters puts the long-term inflation expectation at 2.30%, yielding a real risk free rate of -1.7%.
U.S. stocks. Based on data from Shiller the volatility of U.S. large cap stocks over the period 1970-2016 was 16.8%. I don't sample a larger range because volatility has dropped due to economic and financial changes that have occurred. According to the partially disproved Capital Asset Pricing Model, assuming all risk is systematic risk, the expected premium above the risk free rate scales linearly with volatility. Thus the expected arithmetic return for stocks is:
This estimate doesn't take current valuation levels into consideration. An alternative approach that does take current valuation levels into consideration is to use the Gordon Growth Model equation:
Using Shiller's data, at the end of 2016 the dividend yield was 2.0%, and the real dividend growth rate over 1970-2016 was 1.7%.
The Gordon Growth Model can strictly only be applied to constant growth. And worse, companies may have long periods of time when increased earnings are not being paid out as increased dividends.
Instead of using dividends, it is possible to recast the Gordon Growth Model using earnings:
Like the Gordon Growth Model, this equation only applies to constant growth, and also requires the return on equity be equal to the cost of equity. As of March 12, 2017, this equation gives:
Instead of seeking mathematical truth, we can use a rule-of-thumb based on the observation that when prices are high future returns have been low, and when prices are low, future returns have been high. The rule-of-thumb might get codified as:
where PE10 is the current price divided by average earnings over the last 10 years. This is similar to the previous equation, except that by using E10 instead of current period earnings we are smoothing out volatility associated with the business cycle. As of March 12, 2017, the PE10 was 29.23.
A problem with the PE10 model is, lacking a solid mathematical foundation, there is no solid reason to believe it will still work.
These four estimates are broadly similar. I chose to use the first of the estimates primarily because it incorporates volatility.
U.S. stocks: 4.5% arithmetic mean, 16.8% volatility, 3.2% geometric mean.
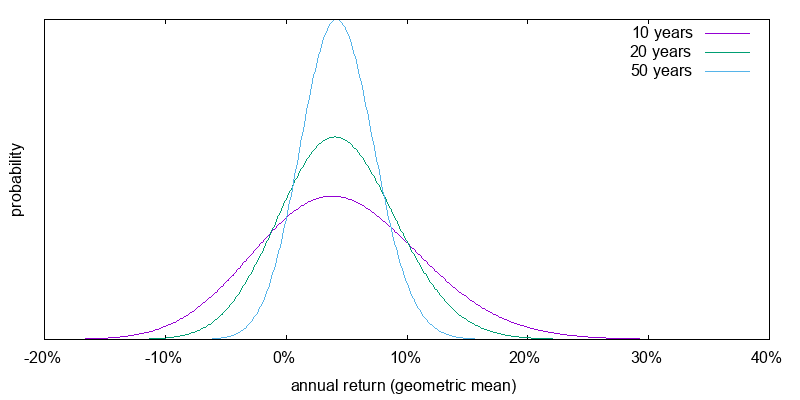
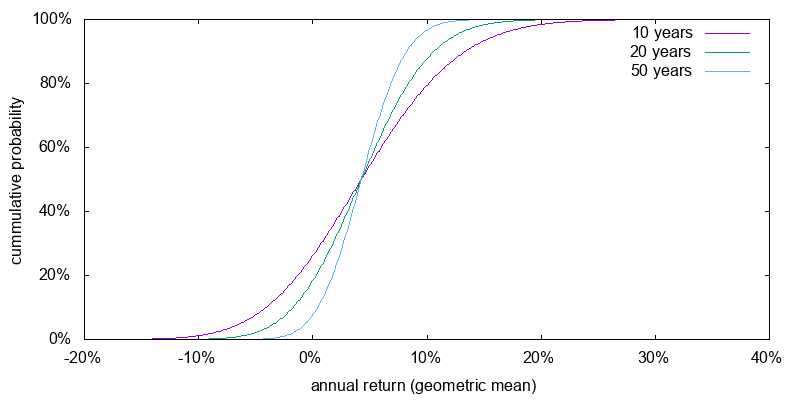
U.S. small cap value. The volatility of small cap value has dropped significantly over the past 90 years. Here I base my core analysis on period after the small cap value effect was widely reported. Based on data from Fama and French U.S. small cap value experienced a volatility of 22.2% over the period 1995-2016. Assuming all the volatility of small cap value represents systematic volatility, and plugging 22.2% into the prior formula gives:
U.S. small cap value: 6.5% arithmetic mean, 22.2% volatility, 4.3% geometric mean.
Note that over this period the risk free rate was 0.2%, so the expected arithmetic return based on volatility considerations is 8.4%, but small cap value actually achieved 14.0%, an unexpected gain of 5.6%. This period is too short to know if there is a non-volatility-based small cap value anomaly, after all the standard error is 4.7%. It would take 63 years before a gain of this size achieved statistical significance.
Dividing history up into three periods: 1927-1980, 1981-1994, and 1995-2016, representing the periods before, during the discovery of, and after the small and value effects were widely known, the risk adjusted outperformance of small cap value compared to the World experience has been: 3.2%, 5.1%, and 5.6%. Thus, if there is a non-volatility-based small cap value anomaly so far there isn't any evidence of it disappearing since it was widely publicized.
Note that the assumption that all volatility of small cap value represents systematic volatility is false. The correlation coefficient between small cap value and stocks was only 0.64 over the period considered. If I were to take this into account I would get a lower estimate for the returns of small cap value. This represents the failure of the Capital Asset Pricing Model. Instead I need to justify my calculations by arguing investors demand similar Sharpe ratios for different asset classes.
60/40 stocks/bonds portfolio. This is considered representative of a typical retirement portfolio, and is not something to be emulated by an effective altruist investor. The average government bond has a maturity of around 7 years. As of March 2017, the 7 year bond was yielding 2.3% nominal, or 0.0% real. Investing in the broader bond market you might do an average of 0.6% better than this. Based on data from Shiller the 10 year bonds volatility was 10.3% over the period 1970-2016. Loosely conflating maturity with duration this would put the volatility of a 7 year bond at 7.2%. Assuming stocks and bonds are uncorrelated this would then give:
60/40 stocks bonds portfolio: 2.9% arithmetic mean, 10.5% volatility, 2.4% geometric mean.
Apart from the now somewhat dated publication by Dimson, Marsh, and Staunton, I don't have access to data sources for stock market returns besides the U.S.. They are expected to be broadly similar on a risk adjusted basis to those within the U.S.. However, because the capital structure of firms differs across countries, there is no reason to believe that the volatility, and hence the expected return of various asset classes will be the same.
You may be wondering why I did not add buybacks to dividends in the Gordon Growth Model equation. To put it simply, buybacks are not a form of dividend. Assuming a company is fairly valued, buybacks do not influence the share price. Buy and hold investors receive nothing. They own a larger share of a smaller pie. Investors who take part in the buyback and sell their shares receive cash, but they no longer own any dividend paying shares. To count dividends and then add buybacks is to have your cake and eat it too. If you must count buybacks, you also need to factor in the share count reduction that is occurring and that reduces aggregate earnings and dividends. An example will make things clear. Imagine a company with $1m in long-term assets that earn 9% per year, and $1m in cash that earns 1% per year. The company has 100 shares outstanding, and uses all of its available cash to perform a buyback. Since the cash earns 1% per year and the remaining assets earn 9%, the shareholders will give up 10% of their shares in exchange for the cash. This preserves the earnings per share. Afterwards there are 10 former shareholders with $1m earning 1% and 90 shares backed by $1m in assets earning 9%. Beforehand we had 100 shares of $2m earning 5%. Each of these three positions is equivalent, earning $1k per share per year. The buyback had no effect.
Time is a diversifier, but only a weak one. Over any reasonable period investing entails the risk that you will end up with less than you started with. Figures 1 and 2 show the return probabilities for U.S. stocks and U.S. small cap value that we just estimated over 10, 20, and 50 years. Even over a 50 year period there is a significant chance of receiving a negative real return.


A typical effective altruism portfolio might consist of one to three index funds, chosen from a domestic stock fund, an international stock fund, a global stock fund, and a small cap value fund.
It is important to invest with someone you can trust, and sadly the ultimate goal of most brokers and financial advisors is their own self enrichment. In the U.S. the Vanguard Group has made a name for itself as a quasi not-for-profit, low-cost, no frills, investment group that sits on the same side of the table as the investor. They have sister financial organizations at various levels of maturity in over 20 countries.
In the U.S. Vanguard offers 3 different funds which they label as small cap value funds: VSIAX/VBR, VIOV, and VTWV. By far the largest, and the one Vanguard will steer you towards is VSIAX/VBR. Unfortunately this fund is best thought of as a blend of small cap value and medium cap value funds. The assets under management for VIOV and VTWV are very small, meaning it might be possible they could go away in the future. And VTWV is heavily weighted towards financials; comprising 41% of the fund on 2020-03-31. As a result I would recommend using VIOV. Alternatively you could consider using Vanguard's value factor fund, VFVA, which has a higher weighting on value but a lower weighting on small.
You need to decide whether to manage effective altruism funds in a separate account from your personal funds. There are advantages and disadvantages to both strategies. I won't list them here.
When you have a large sum that you wish to invest, you have the option of dollar cost averaging, by spreading the purchase out over time. This ensures that you don't get into the market at the one worst possible point, but delays how long it takes before you are fully in the market. Because effective altruists are more expected-return maximizers, rather than risk minimizers, dollar cost averaging is the wrong strategy.
Stocks pay dividends, and when you sell them you realize a capital gain or loss. Paying attention to the tax ramifications of this is part of the art of investing. Capital gains and losses should be offset when possible. Capital gains should be delayed by buying and holding. Lot based accounting of mutual funds should be used as it provides more opportunities for tax management. Dividends and capital gains should be paid to cash rather than reinvested to simplify lot management.
Tax advantaged accounts allow one to delay or avoid taxes. The problem is they are normally geared towards saving for retirement. In the U.S.. an early withdrawal penalty is assessed if money is withdrawn before age 59 1/2. As such tax advantaged accounts are not usually appropriate for effective altruist savings.
The U.S. tax code allows an itemized tax deduction for donations to recognized charities. If you do not normally itemize because your itemized deductions are less than the standard deduction, it might be a good idea to bunch multiple years of donations into a single tax year in order to be able to take advantage of this tax deduction.
In the U.S. you can donate appreciated shares to a public charity and claim the full appreciated value as an itemized tax deduction without ever having to realize a capital gain. This deduction is limited to 30% of your adjusted gross income when donating to public charities, or 20% when donating to private foundations, with a five-year carry forward of amounts above the limit. This favorable tax treatment should be taken advantage of by donating your most appreciated assets to charity, provided the recipient is able to handle it.
In the U.S. private foundations and donor advised funds can be used to commit to giving today, realize a tax deduction today, but delay deciding on the recipient organization until tomorrow. For the effective altruist who has received a windfall, and wishes to give to effective altruism causes, but wants to wait until the effective altruism landscape clears up, this arrangement might seem ideal. But there are some significant caveats:
In summary, private foundations probably don't make sense for less than $1-2 million in assets. Donor advised funds can be appropriate for smaller amounts, but only if you are willing to work within the constraints they impose.
What about using leverage to effectively hold more than 100% stocks? Three possibilities are leveraged ETFs, margin, and options. These are advanced topics that shouldn't be attempted before you have mastered other aspects of investing. In evaluating leverage it is vital not to confuse ex-ante strategy and ex-post outcomes. When you employ a significant amount of leverage you are quite likely to get returns that are either very good or very bad, but this says nothing about the quality of the strategy you employed.
Leverage is not a magic formula to getting rich. What it involves is receiving higher expected returns in exchange for a higher probability that those expected returns never materialize.
Figure 3 shows the expected return for a 300% U.S. stocks portfolio in which the margin borrowing rate was -0.8% real. This represents the current margin rate. It is the Interactive Brokers rate on June 16, 2017, for a $100k to $1m margin loan of 2.16% nominal, less the Survey of Professional Forecasters 2017Q2 projected 2017 inflation rate of 2.3%. The expected returns have widened significantly in comparison to 100% U.S. stocks.
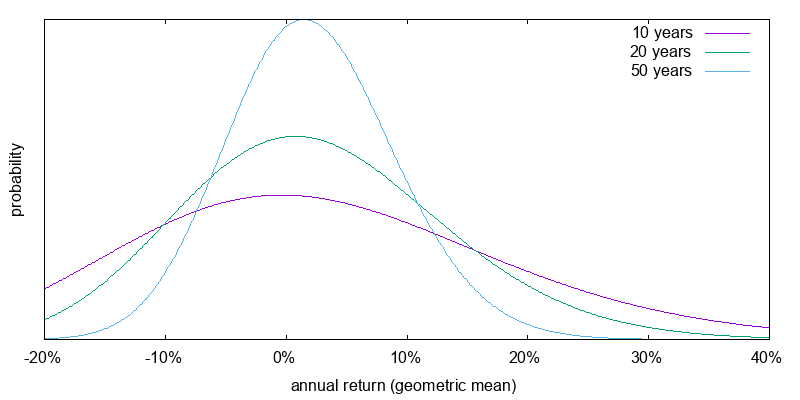
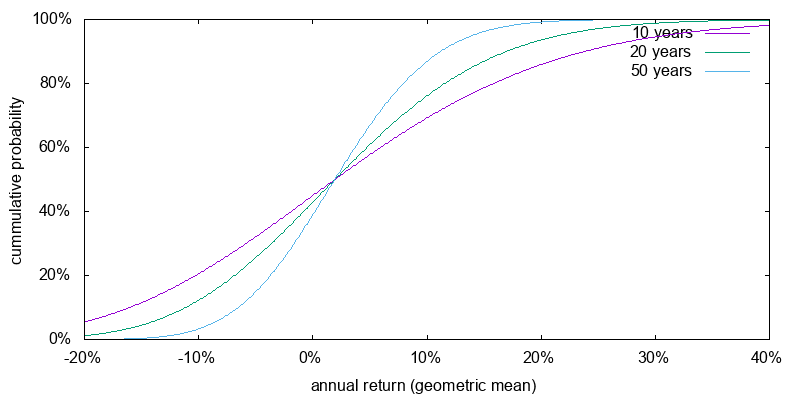
Figure 4 shows the expected return for a 300% U.S. stocks portfolio in which the margin borrowing rate was 2.2% real. This represents the margin rate in average times past. It is the average risk free rate reported by Dimson, Marsh, and Staunton for 1900-2000 of 0.9%, plus the Interactive Brokers markup above their benchmark rate for a $100k to $1m margin loan of 1.0%, plus the difference between their benchmark rate of 1.16%, and nominal short term Treasuries at 0.85% on June 16, 2017. Comparison to 100% U.S. stocks, the expected returns have widened and shifted to the right. The situation is bleak, but not perhaps as bleak to the effective altruist as it may first appear. Since an effective altruist places less weight on downside risk measures, a broadening of the geometric mean expected return is likely to have an overall positive effect on the cause they care about. That is, the probability of receiving 10% above the geometric mean for 50 years more than compensates for the equal probability of receiving 10% below the geometric mean for 50 years.
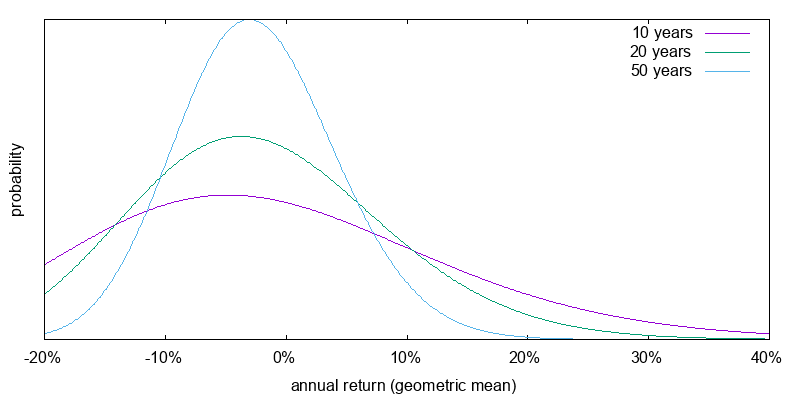
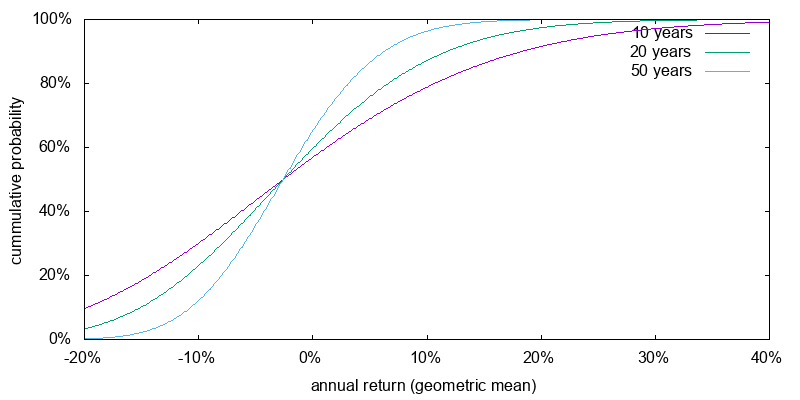
Money is currently cheap, and whether interests rates will revert to those of times past isn't know. What this exercise shows however is if you plan to employ leverage the cost of doing so matters critically.
It is worth mentioning that the widening of the returns distribution has some pretty sobering effects. Taking the more promising -0.8% real margin rate, there is a non-zero chance of -10% annual returns for 50 years, which would reduce a portfolio to below 1% of its original value. Leverage shouldn't be attempted if you are not comfortable with this.
Leveraged ETFs multiply the returns of an index typically by a factor of 2 or 3. Leveraged ETFs return higher returns when times are good at the cost of worse returns when times are bad. Because of increased volatility the mean is boosted more than the median, which may even decline. This makes leveraged ETFs unsuitable for many investors, but the risk profile is acceptable to effective altruists.
I analyze leveraged ETFs in detail in Effective Altruism Investing Strategies: Leveraged ETFs. Due to an annual performance lag of 1.4% to 1.8%, I find them only slightly superior to, or significantly inferior to, investing in small cap value.
The first big problem with buying on margin is the interest rate charged is usually exorbitant, typically 6-7% above the risk free rate. This makes buying on margin a losing proposition. The one exception to this in the U.S. is Interactive Brokers whose margin rates are in the range 1.0-1.5% above the risk free rate. Note that in the U.S. margin interest is tax deductible provided you itemize your deductions.
The second big problem with buying on margin is it is an active strategy which requires continuous, perhaps monthly monitoring, buying, and selling, to maintain the target asset allocation.
Before buying on margin it makes sense to optimize complementarities between your personal investments and effective altruism investments. For instance it typically doesn't make overall sense to hold short term bonds in your personal account, while borrowing on margin and paying margin interest in your effective altruism account. It is better to cut out the middleman and have you effective altruism account pay your personal account for the privilege of borrowing from it.
I haven't attempted to use margin for effective altruism investments, but if you do it seems Interactive Brokers would be the way to go.
Call and put options give you the right, but not the obligation, to buy or sell a particular stock at a particular price on, or before, some some date. By purchasing deep in the money calls it is possible to obtain a leveraged position.
I analyze the use of deep in-the-money call options in Effective Altruism Investing Strategies: Stock Options. Due to the high price of deep in-the-money call options I find their use inferior to investing in small cap value.
Personal investing for retirement is very different from investing for effective altruism causes. Retirement investing is best approached, at least partially, as a liability matching exercise. Paying off debts and building up equity in a home is usually a good start. Depending upon the expected Social Security payments, there is often the need for some bonds in a retirement portfolio to get the appropriate level of risk. Despite their prevalence, constant maturity bond funds are not appropriate for a retirement portfolio. Individual bonds, especially inflation indexed bonds, that match the duration of your retirement liabilities are more appropriate. Defined maturity bond funds would also be appropriate, but aren't available with sufficiently long durations. Fixed income assets should probably be annuitized to purchase an income annuity at around age 65, and stocks at around age 80. Don't buy any other form of annuity.
I have a fungible border between personal investments and effective altruism investments. On the solidly personal side I have Social Security, an inflation indexed income annuity, and 30 year inflation indexed bonds to at least notionally provide for consumption in retirement. For consumption prior to that and effective altruism causes for the past 3 years I have been 100% invested in a small cap value mutual fund. I also have a small private foundation which is 80% invested in small cap value, and 20% invested in bonds.
I am interested in increasing the expected returns associated with my current effective altruism investments in exchange for increased risk. However the 2% volatility based increase of small cap value over U.S. stocks, and the possibility of there being a 3-5% small cap value anomaly, leave me a little hesitant. More signifcantly, I have been unable to identify a suitable vehicle for obtaining 300% stocks. The unlimited downside of trading on margin rules it out, and neither leveraged ETFs, nor options appear like a win.
© 2016-2017 Gordon Irlam. Some rights reserved.
 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.